By Caitlin French

Introduction to Special Relativity

Special relativity, developed by Albert Einstein in 1905, completely transformed our ideas about space and time. Although Newtonian mechanics provides good approximations at low speeds, Einstein corrected mechanics in order to handle situations involving motion near the speed of light. Einstein replaced the Galilean transformations of Newtonian mechanics with the Lorentz transformations in his theory of Special Relativity.

Einstein’s theory is based on two main postulates, from which many interesting things follow. But the main idea of Special Relativity is that, if you move fast enough through space, the observations you make about space and time differ from the observations of other people who are moving at different speeds.

The Two Postulates of Special Relativity

Special Relativity is based on two postulates:

1. The laws of physics are invariant (identical) in all inertial systems (non-accelerating frames of reference moving at a constant speed).

2. The speed of light (c) in a vacuum is the same in all frames of reference, regardless of motion relative to the light source. This is required for the laws of electrodynamics to apply equally for all frames.

Searching for the Aether

Are you moving right now? In your current reference frame, you may think you are stationary. However, relative to something floating in space, you are moving: you are sitting on the Earth, which is rotating on its axis and orbiting the Sun at 30kms^-1. This made people think: is there an absolute reference frame against which to measure all motion? Is there something in the universe which is always stationary? Physicists postulated a “luminiferous aether”: a stationary, absolute reference frame which is also a medium for light waves to travel through.

Experiments at the time, such as the Michelson-Morley experiment, had results which suggested that the Earth was always stationary relative to the aether – something which was difficult to explain. But Einstein’s solution was to discard the notion of an aether and instead say that all motion is relative.

The Michelson-Morley Experiment

The Michelson-Morley experiment was conducted to settle the debate about the aether. It involved a beam of light splitting at a beam splitter (a half-silvered mirror), where one beam travels parallel to the supposed “aether drift” (which we take to be along the horizontal line from the source to the mirror) and the other perpendicular, where the distance between the beam splitter and both mirrors is the same. The two beams reflect off the mirrors, recombine at the beam splitter and then travel to a detector where an interference pattern forms. If the equipment is at rest in the aether, then the times for the light beams to travel from the source to the detector will be equal, so the light beams will constructively interfere. However, if the apparatus moves to the right with velocity u relative to the aether, then there will be a difference in the times. Any difference in time for the beams to travel to the detector means a change in phase, and therefore a different interference pattern.

We can think of an analogy of boats on a river, where there is a current to the right (the aether drift). For the boat travelling parallel to the current, the amount it is aided by the current on the way out is cancelled by the amount it is slowed down on the way back. For the boat travelling perpendicular to the current, it has to travel a little further as it has to aim slightly to the side, so it takes longer to travel out and back.

Looking at the horizontal beam:

The time taken to go from A to B is t₁ and the time for return is t₂. The distance travelled from A to B is L + ut₁ (Shown by the top red arrow. This is the fixed distance between the mirrors added to the distance travelled by the mirrors in the time t₁ using distance = speed x time). This will be equal to the distance ct₁ (c, the speed of light, multiplied by time).

In a similar way, we can write an equation for the return distance, but this time we subtract ut₂.

This gives us the total time to travel from A to B and back again, which is t₁ + t₂:

ct₁ = L + ut₁t₁= L / (c - u)

ct₂= L – ut₂ t₂ = L / (c + u)

t₁ + t₂ = L / (c - u) + L / (c + u) = 2Lc / (c²- u²)

Dividing the numerator and denominator by c², we get:

$t_{1} + t_{2} = \frac{\frac{2L}{c}}{1-\frac{u^{2}}{c_{2}}}$

Now looking at the vertical beam:

You can see from the diagram that, relative to the stationary aether, the light travels along the hypotenuse of a right-angled triangle. We use Pythagoras’ theorem to form an equation, which we then rearrange for time, and multiply by two (as the light must travel from A to C and back again). So:

(ct₃)² = L² + (ut₃)² (Pythagoras)

L² = c²t₃² – u²t₃² = (c² – u²)t₃²

t₃ = L/√(c² – u²)

2t₃ = 2L/√(c² – u²)

Dividing the numerator and denominator by √(c²), we get:

$2t_{3} = \frac{\frac{2L}{c}}{\sqrt{1-\frac{u^{2}}{c_{2}}}}$

But, these times are not equal: t₁ + t₂ ≠ 2t₃. They are wrong by a factor of:

$\frac{1}{\sqrt{1-\frac{u^{2}}{c_{2}}}} = \gamma$

From our calculations, we would expect some interference effects to be detected. However, experimentally, this was not the case. Experimentally, no time difference was found – the velocity of the Earth through the aether could not be detected. There was no aether!

The Problem with Newtonian Mechanics

In Newtonian mechanics, we add velocities. Consider a car approaching you at 30ms^-1. A passenger throws a ball towards you at 5ms^-1. The ball travels at 5ms^-1 relative to the passenger. However, if you measure the speed of the ball, it approaches you at 30 + 5 = 35ms^-1.

Now if the car approaches you at 30ms^-1and turns on the headlights, at what speed does the light approach you? Applying the same logic, we would expect it to be travelling at c (3.0 x 10⁸ms^-1) + 30 = 300,000,030 ms^-1, which is faster than the speed of light, which isn’t possible!

As speed is distance/time, that means there is something wrong with our notion of distance and time.

Lorentz Transformations

Einstein said that there are actually four dimensions, three of which are spatial dimensions (up/down, left/right, forward/backward) and one is time. We define an event to have spacetime coordinates (t,x,y,z) in system S and (t’,x’,y’,z’) in S’, where S and S’ are two inertial frames of reference.

An un-primed variable (without a dash) is a measurement relative to you, whilst a primed variable (with a dash) is a measurement relative to the object you are measuring.

We are only considering relative motion parallel to the x-axis, so only the x and t coordinates are transformed, whilst the y and z coordinates remain unaffected.

Lorentz Transformation

We assume that a transformation γ is performed on the distance x’ + vt’ (adding the vt’ to account for the motion of the object) to give us x.

x = γ(x’ + vt’)

x’ = γ(x-vt)

To go from a primed (S’) to an un-primed (S) frame, switch the primed and un-primed variables and change the sign of velocity v. This is because, if the S’ frame is moving right with respect to the S frame, then the S frame is moving left with respect to the S’ frame.

If a light beam travels in both frames and we assume the speed of light is constant in all frames:

x = ct

x’ = ct’

Which implies:

ct = γ(ct’ + vt’) ⇒ ct = γ(c + v)t’

ct’ = γ(ct – vt) ⇒ ct’ = γ(c – v)t

Multiplying these together:

ct(ct’) = γ²(c + v)(c – v)tt’ ⇒ c² = γ²(c² – v²)

From this we can derive the Lorentz Transformation:

$\gamma = \frac{1}{\sqrt{1-\frac{v^{2}}{c_{2}}}}$

So:

$x = \frac{x'+vt'}{\sqrt{1-\frac{v^{2}}{c_{2}}}} = \gamma (x'+vt')$

$x' = \frac{x-vt}{\sqrt{1-\frac{v^{2}}{c_{2}}}} = \gamma (x-vt)$

Time dilation

Time Transformation

By squaring γ and rearranging, you can show that:

(1 – γ²) = - (v²γ²)/c²

We now set up a different equation where we substitute x into the equation for x’:

x’ = γ(x – vt) ⇒ x’ = γ(γ(x’ + vt’) – vt)

Multiplying out, rearranging and substituting in our result for (1-γ²):

γvt = γ²vt’ – x’(1 – γ²) = γ²vt’ + (v²γ²x’)/c²

Solving for t:

t = γ(t’ + vx’/c²)

t’ = γ(t – vx/c²)

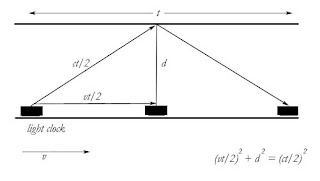
Light Clock

If a clock is in motion, then relative to another observer, time passing on the clock slows down. Note that, as far as the clock is concerned, in its frame of reference, time passes at the same rate. So, time slows as speed increases only when viewed from another frame of reference.

Let’s use the example of a light clock, where, from the clock’s own reference frame, a light beam bounces up and down as it is reflected between 2 mirrors. However, from the point of view of an observer on the ground who watches the clock move past with a velocity v, the light beam appears to take a diagonal path.

From the point of view of the moving clock, the time for the light to travel up and then down is:

t’ = 2d/c

From the point of view of someone on the ground, this time is (using pythagoras, just as we did to explain the Michelson Morley experiment):

(cΔt/2)² = d² + (vΔt/2)²

Multiplying through by 4 and rearranging for t’²:

Δt² = 4d²/(c² – v²)

Taking c² out of the denominator and square rooting:

$\Delta t = \sqrt{\frac{4d^{2}}{c^{2}(1-\frac{v^{2}}{c^{2}})}}$

Therefore:

$\Delta t = \frac{2d}{c} \frac{1}{\sqrt{1-\frac{v^{2}}{c_{2}}}} = \Delta t' \frac{1}{\sqrt{1-\frac{v^{2}}{c_{2}}}}$

∆t=γ∆t'

If we plug in the speed of light, c, into the formula, the time dilation factor becomes infinite, so time stands still.

Examples

Time dilation explains the presence of cosmic ray muons reaching the Earth’s surface. Mesons are particles which spontaneously decay after an average lifetime of 2 microseconds, meaning they should only be able to travel about 600m from the top of the Earth’s atmosphere. However, the distance from the atmosphere to the Earth’s surface is 10km – much longer. So how can we still detect muons? Muons travel close to the speed of light, so, from our point of view, time passes more slowly for them, so they live for long enough to travel the 10km distance.

Time dilation also raises an interesting question in the twin paradox. Imagine the situation where a twin (Amy) flies off in a spaceship travelling near the speed of light, leaving her twin (Bob) on Earth. On Amy’s return, she discovers that Bob, who stayed on Earth, has aged much more. This has been explained using the fact that Amy travelled at a very fast speed, so from Bob’s point of view, Amy’s time passed more slowly, so Amy aged less. But there is a problem: we could say that, from Amy’s point of view, Bob travelled away at a very fast speed, so Bob’s time passed more slowly, so Bob aged less. However, this is not really a paradox. The answer is that, if this were possible, Amy would age less, but for a different reason: in order to return to Earth, she must decelerate, turn around and then accelerate back, causing her to age less.

Length Contraction

When an object is in motion, its measured length, relative to another observer, shrinks in the direction of its motion. Note that, as far as the object is concerned, in its frame of reference, it remains the same size. So, objects shorten as speed increases only when viewed from another frame of reference. For instance, if we are stationary on the ground and watch a spaceship fly past at a speed close to the speed of light, the people on the spaceship will think that the spaceship is the same length as it is when it is stationary, whilst it will appear shorter to you.

If a light pulse is fired from the back to the front of a train and is reflected back, with Amy standing on the train and Bob watching from the ground as the train travels past, the time measured by Amy is:

Δt’ = 2L’/c

We can then use the equation to get the time for Bob:

∆t= γ∆t'= γ 2L'/c

From Bob’s point of view, when the pulse is travelling with the train (t’¹), the time will be longer, whilst when the pulse is travelling in the opposite direction to the train (t’²), the time will be shorter.

Returning to our example of the Michelson-Morley experiment, where we got the result:

$t_{1} + t_{2} = \frac{\frac{2L}{c}}{1-\frac{v^{2}}{c_{2}}} = \frac{2L}{c} \gamma ^{2}$

We then set these times equal to each other, so we get:

(2L/c)γ² = γ(2L'/c)

So therefore:

$L = \frac{L'}{\gamma } = L' \sqrt{1-\frac{v^{2}}{c_{2}}}$

This shows that the length of the train is different in different inertial frames of reference. As γ > 1, L < L’ meaning the length L as measured by the outside observer is less than the length of the object with respect to itself. This explains the name of this effect: length contraction.

If the spaceship was approaching the speed of light, then, measured relative to you as you stand on the ground, its length would shrink to nothing. If v (the speed of the spaceship) approaches c (the speed of light), then 1/γ approaches 0, so L (as measured by you) approaches 0.

The Relativistic Velocity Addition Formula

Using the effects of length contraction and time dilation, x = γ(x’ + vt’) and t = γ(t’ + vx’/c²), we get:

$u = \frac{\Delta x}{\Delta t} = \frac{\gamma (\Delta x' + v\Delta t')}{\gamma (\Delta t' + \frac{v}{c^{2}}\Delta x')}$

$u = \frac{\gamma (\Delta t'(\frac{\Delta x'}{\Delta t'} + v)}{\gamma \Delta t'(1+ \frac{v}{c^{2}}\frac{\Delta x'}{\Delta t'})}$

$u = \frac{(u'+v)}{(1+ \frac{v}{c^{2}}u')}$

$u' = \frac{(u-v)}{(1- \frac{v}{c^{2}}u)}$

Imagine a spaceship travelling at half the speed of light, which then transmits a light pulse at half the speed of light relative to the spaceship. According to Newtonian mechanics, these velocities would add to c. But using the relativistic velocity addition formula where v = u’ = c/2:

u = (c/2+ c/2)/(1+ 1/4)= 4/5 c

It would actually travel at 4/5 the speed of light.

The Universal Speed Limit

If a spaceship moving at a velocity v transmits a light pulse at speed c, we can show that the light pulse will always travel at the velocity c in all reference frames. If we use the velocity addition formula for any v, making u’ equal to c:

u = (c+v)/(1+ vc/c²) = (c+v)/c(c+v) = c

Whatever the speed the spaceship is moving at, the speed of the transmitted light pulse will always be c.

Contrary to popular belief, it is possible to be travelling faster than the speed of light, but we have not yet discovered anything which does travel faster than light. However, what is impossible is to accelerate to or past the speed of light. This is because, as the speed of an object approaches c, from an observer’s point of view, relativistic mass increases, meaning an infinite amount of energy is needed to make the object faster from within the observer’s frame of reference.

Relativity of Simultaneity

Another consequence of relativity theory is that there is no such thing as simultaneity between two events when viewed in different frames of reference.

Imagine a train moving at a constant speed with a torch in the middle. Amy stands on the train holding the torch, whilst Bob watches from the ground. Two light pulses are simultaneously sent out to the front and back of the train. Imagine this is a universe where the speed of light is much slower so that the time the light reaches each of the ends can be easily measured. From Amy’s point of view, the light reaches both ends at the same time. This is no surprise because the distances the light travels and the speed of light is the same:

t’_left = t’_right = L’/2c

However, from Bob’s point of view, these times are different. If the torch is turned on when Amy passes Bob so that the front end of the train moves away from Bob and the back end of the train moves towards Bob, then from Bob’s point of view, the light hits the back of the train first since it has a shorter distance to travel. They do not agree about the time of an events.

From Bob’s point of view:

t_left = (L/2)(1/(c+v))

t_right = (L/2)(1/(c-v))

Whilst these two events are simultaneous from Amy’s point of view, they do not occur at the same time for Bob. This shows that the order events happen in is different in different reference frames. There is no absolute time!

An interesting example of length contraction is the ladder-garage paradox. A person claims that they can fit a 20m ladder into a 10m garage, despite the fact that, when stationary, the ladder is much longer than the length of the garage. Imagine that there are guillotines at either side of the garage which are released when the ladder is inside the garage. When someone runs at a speed close to the speed of light towards the garage, from the garage’s reference frame, the length of the ladder would decrease so that it would be able to fit, and would not be cut by the guillotines. However, from the ladder’s reference frame, the length of the garage would decrease so that the ladder would not be able to fit and would be cut by the guillotines. This creates a paradox. However, the solution to this paradox is explained by relativity of simultaneity. The answer is that the ladder is not cut by the guillotines. From the point of view of the garage, the ladder shrinks and fits inside. From the point of view of the person with the ladder, the guillotines drop at different times. As the ladder approaches the garage, the front guillotine comes down and goes back up again. After the ladder has passed the back of the garage, the back guillotine then comes down and misses the ladder. The paradox is resolved, but only as a result of realising that simultaneity of events is no longer true in special relativity!